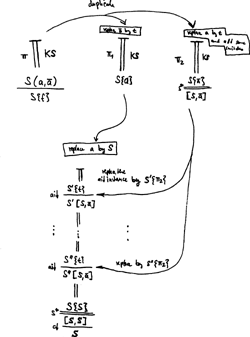
System SKS is a set of rules for classical propositional logic presented in the calculus of structures. Like sequent systems and unlike natural deduction systems, it has an explicit cut rule, which is admissible. In contrast to sequent systems, the cut rule can easily be restricted to atoms. This allows for a very simple cut elimination procedure based on plugging in parts of a proof, like normalisation in natural deduction and unlike cut elimination in the sequent calculus. It should thus be a good common starting point for investigations into both proof search as computation and proof normalisation as computation.

Pdf 10 April 2003
CSL 2003, LNCS 2803, pp. 86–97

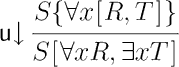
In this paper we will see deductive systems for classical propositional and predicate logic in the calculus of structures. Like sequent systems, they have a cut rule which is admissible. Unlike sequent systems, they drop the restriction that rules only apply to the main connective of a formula: their rules apply anywhere deeply inside a formula. This allows to observe very clearly the symmetry between identity axiom and the cut rule. This symmetry allows to reduce the cut rule to atomic form in a way which is dual to reducing the identity axiom to atomic form. We also reduce weakening and even contraction to atomic form. This leads to inference rules that are local: they do not require the inspection of expressions of arbitrary size.

Pdf 10 March 2006
Notre Dame Journal of Formal Logic, Vol. 47, No. 4, pp. 557–580, 2006

Deep inference is a natural generalisation of the one-sided sequent calculus where rules are allowed to apply deeply inside formulas, much like rewrite rules in term rewriting. This freedom in applying inference rules allows to express logical systems that are difficult or impossible to express in the cut-free sequent calculus and it also allows for a more fine-grained analysis of derivations than the sequent calculus. However, the same freedom also makes it harder to carry out this analysis, in particular it is harder to design cut elimination procedures. In this paper we see a cut elimination procedure for a deep inference system for classical predicate logic. As a consequence we derive Herbrand's Theorem, which we express as a factorisation of derivations.

Pdf 9 March 2005
Studia Logica, Vol. 82, No. 1, pp. 51–71, 2006

We introduce diagrams, called 'atomic flows', that forget much of the syntactic structure of derivations and only retain causal relations between atoms. Using atomic flows on propositional logic, we can design and control several normalisation procedures. In particular, we can obtain cut elimination as a special case of more general normal forms. This technique only relies on substituting derivations in the place of atoms, similarly to natural deduction, and not on permuting inference steps, as in the sequent calculus. Because they abstract away from most syntactic details, atomic flows allow for very simple control of normalisation procedures, which would otherwise be cumbersome in the bare syntax. We operate in deep inference, a very general methodology, where normalisation is more difficult to control than in other syntactic paradigms.

Pdf 21 July 2007
Submitted

This paper presents systems for first-order intuitionistic logic and several of its extensions in which all the propositional rules are local, in the sense that, in applying the rules of the system, one needs only a fixed amount of information about the logical expressions involved. The main source of non-locality is the contraction rules. We show that the contraction rules can be restricted to the atomic ones, provided we employ deep-inference, i.e., to allow rules to apply anywhere inside logical expressions. We further show that the use of deep inference allows for modular extensions of intuitionistic logic to Dummett's intermediate logic LC, Gödel logic and classical logic. We present the systems in the calculus of structures, a proof theoretic formalism which supports deep-inference. Cut elimination for these systems are proved indirectly by simulating the cut-free sequent systems, or the hypersequent systems in the cases of Dummett's LC and Gödel logic, in the cut free systems in the calculus of structures.

Conference version pdf 9 August 2006
LPAR 2006, LNCS 4246, pp. 242–256

Full paper pdf 9 August 2006

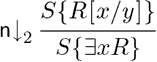
We present an inference system for classical first order logic in which each inference rule, including the cut, only has a finite set of premises to choose from. The main conceptual contribution of this paper is the possibility of separating different sources of infinite choice, which happen to be entangled in the traditional cut rule.

Pdf 1 December 2003
Presented at First Order Logic 75 under the title A Finitary System for First Order Logic; appeared in Hendricks et al., editor, First-Order Logic Revisited, Logos Verlag, Berlin, 2004, pp. 59–74

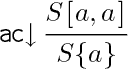
The calculus of structures is a framework for specifying logical systems, which is similar to the one-sided sequent calculus but more general. We present a system of inference rules for propositional classical logic in this new framework and prove cut elimination for it. The system also enjoys a decomposition theorem for derivations that is not available in the sequent calculus. The main novelty of our system is that all the rules are local: contraction, in particular, is reduced to atomic form. This should be interesting for distributed proof-search and also for complexity theory, since the computational cost of applying each rule is bounded.

Pdf 2 October 2001 Now replaced by Locality for Classical Logic
LPAR 2001, LNCS 2250, pp. 347–361

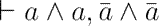
I show two simple limitations of sequent systems with multiplicative context treatment: contraction can neither be restricted to atoms nor to the bottom of a proof tree.

Pdf 24 November 2003
Logic Journal of the Interest Group in Pure and Applied Logics, Vol. 11 No. 5, pp. 525–529

We show how to get consistency for first order classical logic, in a purely syntactic way, without going through cut elimination. The procedure is very simple and it also shows how finitariness is actually a triviality (contrarily to what one would guess from textbooks).

Pdf 10 September 2003 It is contained in A First Order System with Finite Choice of Premises

We obtain two results about the proof complexity of deep inference: 1) deep-inference proof systems are as powerful as Frege ones, including when extended with the Tseitin extension rule and with the substitution rule; 2) there are analytic deep-inference proof systems that exhibit an exponential speed-up over analytic Gentzen proof systems that they polynomially simulate.

Pdf 2 September 2007
Submitted

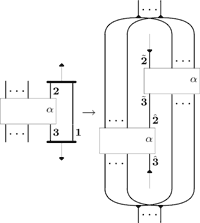
Medial is an inference rule scheme that appears in various deductive systems based on deep inference. In this paper we investigate the properties of medial as rewriting rule independently from logic. We present a graph theoretical criterion for checking whether there exists a medial rewriting path between two formulas. Finally, we return to logic and apply our criterion for giving a combinatorial proof for a decomposition theorem, i.e., proof theoretical statement about syntax.

Pdf 13 April 2007
RTA 2007, LNCS 4533, pp. 344–358

This is a study of the semantics and proof theory of the logic of bunched implications (BI), which is promoted as a logic of (computational) resources, and is a foundational component of separation logic, an approach to program analysis. BI combines an additive, or intuitionistic, fragment with a multiplicative fragment. The additive fragment has full use of the structural rules of weakening and contraction, and the multiplicative fragment has none. Thus it contains two conjunctive and two implicative connectives. At various points, we illustrate a resource view of BI based upon the Kripke resource semantics. Our first original contribution is the formulation of a proof system for BI in the newly developed proof-theoretical formalism of the calculus of structures. The calculus of structures is distinguished by its employment of deep inference, but we already see deep inference in a limited form in the established proof theory for BI. We show that our system is sound with respect to the elementary Kripke resource semantics for BI, and complete with respect to the partially-defined monoid (PDM) semantics. Our second contribution is the development from a semantic standpoint of preliminary ideas for a hybrid logic of bunched implications (HBI). We give a Kripke semantics for HBI in which nominal propositional atoms can be seen as names for resources, rather than as names for locations, as is the case with related proposals for BI-Loc and for intuitionistic hybrid logic. The cost of this approach is the loss of intuitionistic monotonicity in the semantics. But this is perhaps not such a grave loss, given that our guiding analogy is of states of models with resources, rather than with states of knowledge, as is standard for intuitionistic logic.

Pdf June 2007
MSc thesis, successfully defended in August 2007

Cirquent calculus is a new proof-theoretic framework, whose main distinguishing feature is sharing: unlike the more traditional frameworks that manipulate tree- or forest-like objects such as formulas (Frege), sequents (Gentzen), hypersequents (Avron, Pottinger) or structures (Guglielmi), cirquent calculus deals with circuit-style constructs called cirquents, in which children may be shared between different parent nodes. Among its advantages are greater efficiency, flexibility and expressiveness. The approach was born in “Introduction to cirquent calculus and abstract resource semantics” (Journal of Logic and Computation, v. 16). That so far the only paper on the subject introduced cirquent calculus in a special, “shallow” form, where the depths of cirquents were limited to two. While the shallow version of cirquent calculus was sufficient to achieve the main goal of that paper — taming the otherwise wild class of binary tautologies and their instances — the paper also outlined the possibility and expediency of studying more general, deep versions of cirquent calculi. The present article contains a realization of that outline. It elaborates a deep cirquent calculus system CL8 for classical propositional logic and the corresponding fragment of the resource-conscious computability logic. It also shows the existence of polynomial size analytic CL8-proofs of the pigeonhole principle — the family of tautologies known to have no such proofs in traditional systems.

Pdf 18 September 2007
Submitted

In this thesis we see deductive systems for classical propositional and predicate logic which use deep inference, i.e. inference rules apply arbitrarily deep inside formulas, and a certain symmetry, which provides an involution on derivations. Like sequent systems, they have a cut rule which is admissible. Unlike sequent systems, they enjoy various new interesting properties. Not only the identity axiom, but also cut, weakening and even contraction are reducible to atomic form. This leads to inference rules that are local, meaning that the effort of applying them is bounded, and finitary, meaning that, given a conclusion, there is only a finite number of premises to choose from. The systems also enjoy new normal forms for derivations and, in the propositional case, a cut elimination procedure that is drastically simpler than the ones for sequent systems.

Pdf February 2004
PhD thesis, successfully defended on 22.9.2003, published by Logos Verlag
You can buy this book here and here