Commutative/Non-commutative Linear Logic

Alessio Guglielmi's Research / Deep Inference and the Calculus of Structures / Commutative/Non-commutative Linear Logic

We conservatively extend mixed multiplicative and multiplicative exponential linear logic with a self-dual non-commutative operator. The systems so obtained cannot be presented in the sequent calculus, but they enjoy the usual properties of locality, decomposition and cut elimination available in the calculus of structures. We can present Yetter's cyclic linear logic in the calculus of structures and prove cut elimination; interestingly, cyclicity is naturally subsumed by deep inference. New, purely proof-theoretical, techniques are developed for reducing the non-determinism in the calculus of structures.

We introduce the calculus of structures: it is more general than the sequent calculus and it allows for cut elimination and the subformula property. We show a simple extension of multiplicative linear logic, by a self-dual non-commutative operator inspired by CCS, that seems not to be expressible in the sequent calculus. Then we show that multiplicative exponential linear logic benefits from its presentation in the calculus of structures, especially because we can replace the ordinary, global promotion rule by a local version. These formal systems, for which we prove cut elimination, outline a range of techniques and properties that were not previously available. Contrarily to what happens in the sequent calculus, the cut elimination proof is modular.
This paper introduces a logical system, called BV, which extends multiplicative linear logic by a non-commutative self-dual logical operator. This extension is particularly challenging for the sequent calculus, and so far it is not achieved therein. It becomes very natural in a new formalism, called the calculus of structures, which is the main contribution of this work. Structures are formulae subject to certain equational laws typical of sequents. The calculus of structures is obtained by generalising the sequent calculus in such a way that a new top-down symmetry of derivations is observed, and it employs inference rules that rewrite inside structures at any depth. These properties, in addition to allowing the design of BV, yield a modular proof of cut elimination.
Pdf 27 January 2007
ACM Transactions on Computational Logic, Vol. 8 (1:1) 2007, pp. 1–64
The journal version has been butchered by the editorial process, the preprint (linked here) is fine.
This paper studies properties of the logic BV, which is an extension of multiplicative linear logic (MLL) with a self-dual non-commutative operator. BV is presented in the calculus of structures, a proof theoretic formalism that supports deep inference, in which inference rules can be applied anywhere inside logical expressions. The use of deep inference results in a simple logical system for MLL extended with the self-dual non-commutative operator, which has been to date not known to be expressible in sequent calculus. In this paper, deep inference is shown to be crucial for the logic BV, that is, any restriction on the "depth" of the inference rules of BV would result in a strictly less expressive logical system.
Pdf 3 April 2006
Logical Methods in Computer Science, Vol. 2 (2:4) 2006, pp. 1–24
There are pictures that help understanding this paper in Alwen Tiu's MSc thesis Properties of a Logical System in the Calculus of Structures
The calculus of structures is a proof theoretical formalism which generalizes the sequent calculus with the feature of deep inference: In contrast to the sequent calculus, inference rules can be applied at any depth inside a formula, bringing shorter proofs than any other formalisms supporting analytical proofs. However, deep applicability of the inference rules causes greater nondeterminism than in the sequent calculus regarding proof search. In this paper, we introduce a new technique which reduces nondeterminism without breaking proof theoretical properties and provides a more immediate access to shorter proofs. We present this technique on system BV, the smallest technically non-trivial system in the calculus of structures, extending multiplicative linear logic with the rules mix, nullary mix, and a self-dual non-commutative logical operator. Because our technique exploits a scheme common to all the systems in the calculus of structures, we argue that it generalizes to these systems for classical logic, linear logic, and modal logics.
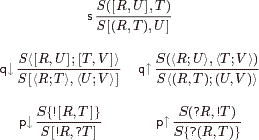
We extend multiplicative exponential linear logic (MELL) by a non-commutative, self-dual logical operator. The extended system, called NEL, is defined in the formalism of the calculus of structures, which is a generalisation of the sequent calculus and provides a more refined analysis of proofs. We should then be able to extend the range of applications of MELL, by modelling a broad notion of sequentiality and providing new properties of proofs. We show some proof theoretical results: decomposition and cut elimination. The new operator represents a significant challenge: to get our results we use here for the first time some novel techniques, which constitute a uniform and modular approach to cut elimination, contrary to what is possible in the sequent calculus.
Conference version pdf 9 August 2002
LPAR 2002, LNCS 2514, pp. 231–246
Full paper pdf 21 January 2004
Submitted to Mathematical Structures in Computer Science
System BV is an extension of multiplicative linear logic (MLL) with the rules mix, nullary mix, and a self-dual, non-commutative logical operator, called seq. While the rules mix and nullary mix extend the deductive system, the operator seq extends the language of MLL. Due to the operator seq, system BV extends the applications of MLL to those where sequential composition is crucial, e.g., concurrency theory. System FBV is an extension of MLL with the rules mix and nullary mix. In this paper, by relying on the fact that system BV is a conservative extension of system FBV, I show that system BV is NP-complete by encoding the 3-Partition problem in FBV. I provide a simple completeness proof of this encoding by resorting to a novel proof theoretical method for reducing the nondeterminism in proof search, which is also of independent interest.
Conference version Pdf 3 June 2005
WoLLIC 2005, Electronic Notes in Theoretical Computer Science 143, 2006, pp. 87–99
Full paper pdf 10 February 2007
To appear on Annals of Pure and Applied Logic
System NEL is a conservative extension of multiplicative exponential linear logic (MELL) by a self-dual non-commutative connective called seq which lives between the par and the times. In this paper, I will show that system NEL is undecidable by encoding two counter machines into NEL. Although the encoding is quite simple, the proof of the faithfulness is a little intricate because there is no sequent calculus and no phase semantics available for NEL.
Conference version pdf 20 August 2003
Presented at WoLLIC 2003 under the title System NEL Is Undecidable, Electronic Notes in Theoretical Computer Science 84
Full paper pdf 12 February 2003
Technical Report WV-03-05, Technische Universität Dresden
In this thesis I study several deductive systems for linear logic, its fragments, and some noncommutative extensions. All systems will be designed within the calculus of structures, which is a proof theoretical formalism for specifying logical systems, in the tradition of Hilbert's formalism, natural deduction, and the sequent calculus. Systems in the calculus of structures are based on two simple principles: deep inference and top-down symmetry. Together they have remarkable consequences for the properties of the logical systems. For example, for linear logic it is possible to design a deductive system, in which all rules are local. In particular, the contraction rule is reduced to an atomic version, and there is no global promotion rule. I will also show an extension of multiplicative exponential linear logic by a noncommutative, self-dual connective which is not representable in the sequent calculus. All systems enjoy the cut elimination property. Moreover, this can be proved independently from the sequent calculus via techniques that are based on the new top-down symmetry. Furthermore, for all systems, I will present several decomposition theorems which constitute a new type of normal form for derivations.
Pdf Pdf in booklet format 25 July 2003
PhD thesis, successfully defended on 24.7.2003

The aim of this work is to give an alternative presentation for the multiplicative fragment of Yetter’s cyclic linear logic. The new presentation is inspired by the calculus of structures, and has the interesting feature of avoiding the cyclic rule. The main point in this work is to show how cyclicity can be substituted by deepness, i.e. the possibility of applying an inference rule at any point of a formula. We finally derive, through a new proof technique, the cut elimination property of the calculus.
Gzipped postscript 19 February 2002
Technical Report WV-01-08, Technische Universität Dresden
Gzipped postscript 19 February 2002
Technical Report WV-01-09, Technische Universität Dresden
This paper has been thoroughly rewritten as A System of Interaction and Structure. The introduction has not been rewritten under the effect of psychotropic substances. Please forget about this paper.
Technical Report WV-99-04, Technische Universität Dresden
The calculus of structures is a new framework for presenting logical systems. It is a generalisation of a traditional framework, the one-sided sequent calculus. One of the main features of the calculus of structures is that the inference rules are deep: they can be applied anywhere inside logical expressions. Rules in the sequent calculus are, in contrast, shallow. A certain logical system in the calculus of structures, called System BV, is studied here. We see that the deep-nesting of rules is a real distinguishing feature between the two frameworks. To this purpose a notion of shallow systems is introduced, such that sequent systems are particular instances. A counterexample, sort of a fractal structure, is then presented to show that there is no shallow system for the logic behind BV, and hence no sequent system for BV. This result contributes to justifying the claim that the calculus of structures is a better logical framework than sequent calculus, for certain logics.
Pdf 12 September 2001 Now replaced by A System of Interaction and Structure II: The Need for Deep-Inference
MSc thesis, successfully defended on 1.8.2001, Technical Report WV-01-06, Technische Universität Dresden
10.10.2007 Alessio Guglielmi email