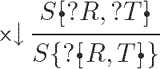
In this paper I will present a deductive system for linear logic, in which all rules are local. In particular, the contraction rule is reduced to an atomic version, and there is no global promotion rule. In order to achieve this, it is necessary to depart from the sequent calculus to the calculus of structures, which is a generalization of the one-sided sequent calculus. In a rule, premise and conclusion are not sequents, but structures, which are expressions that share properties of formulae and sequents.

Conference version pdf 9 August 2002
LPAR 2002, LNCS 2514, pp. 388–402

Full paper pdf 10 June 2002
Technical Report WV-02-01, Technische Universität Dresden

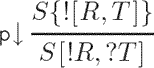
The calculus of structures is a new proof-theoretical framework, like natural deduction, the sequent calculus and proof nets, for specifying logical systems syntactically. In a rule in the calculus of structures, the premise as well as the conclusion are structures, which are expressions that share properties of formulae and sequents. In this paper, I study a system for MELL, the multiplicative exponential fragment of linear logic, in the calculus of structures. It has the following features: a local promotion rule, no non-deterministic splitting of the context in the times rule and a modular proof for the cut-elimination theorem. Further, derivations have a new property, called decomposition, that cannot be observed in any other known proof-theoretical framework.

Pdf 24 November 2003
Theoretical Computer Science, Vol. 309, pp. 213–285

In this thesis I study several deductive systems for linear logic, its fragments, and some noncommutative extensions. All systems will be designed within the calculus of structures, which is a proof theoretical formalism for specifying logical systems, in the tradition of Hilbert's formalism, natural deduction, and the sequent calculus. Systems in the calculus of structures are based on two simple principles: deep inference and top-down symmetry. Together they have remarkable consequences for the properties of the logical systems. For example, for linear logic it is possible to design a deductive system, in which all rules are local. In particular, the contraction rule is reduced to an atomic version, and there is no global promotion rule. I will also show an extension of multiplicative exponential linear logic by a noncommutative, self-dual connective which is not representable in the sequent calculus. All systems enjoy the cut elimination property. Moreover, this can be proved independently from the sequent calculus via techniques that are based on the new top-down symmetry. Furthermore, for all systems, I will present several decomposition theorems which constitute a new type of normal form for derivations.

Pdf Pdf in booklet format 25 July 2003
PhD thesis, successfully defended on 24.7.2003