Modal Logic

Alessio Guglielmi's Research / Deep Inference and the Calculus of Structures / Modal Logic

We can present systematically several normal propositional modal logics, including S5, B and K5, for which cut elimination is proved. We also investigated geometric theories, some of which we expressed in the calculus of structures. A new formalism called 'deep sequents' has been defined, which is especially suitable to modal logics.
We begin by showing how to faithfully encode the Classical Modal Display Logic (CMDL) of Wansing into the Calculus of Structures (CoS) of Guglielmi. Since every CMDL calculus enjoys cut-elimination, we obtain a cut-elimination theorem for all corresponding CoS calculi. We then show how our result leads to a minimal cut-free CoS calculus for modal logic S5. As far as we know, no other existing CoS calculi for S5 enjoy both these properties simultaneously.
Pdf 4 May 2007
Journal of Logic and Computation, Vol. 17 (4) 2007, pp. 767–794

The family of normal propositional modal logic systems is given a very systematic organisation by their model theory. This model theory is generally given using frame semantics, and it is systematic in the sense that for the most important systems we have a clean, exact correspondence between their constitutive axioms as they are usually given in a Hilbert-Lewis style and conditions on the accessibility relation on frames.
By contrast, the usual structural proof theory of modal logic, as given in Gentzen systems, is ad-hoc. While we can formulate several modal logics in the sequent calculus that enjoy cut-elimination, their formalisation arises through system-by-system fine tuning to ensure that the cut-elimination holds, and the correspondence to the formulation in the Hilbert-Lewis systems becomes opaque.
This paper introduces a systematic presentation for the systems K, D, M, S4, and S5 in the calculus of structures, a structural proof theory that employs deep inference. Because of this, we are able to axiomatise the modal logics in a manner directly analogous to the Hilbert-Lewis axiomatisation. We show that the calculus possesses a cut-elimination property directly analogous to cut-elimination for the sequent calculus for these systems, and we discuss the extension to several other modal logics.
Postscript 2 September 2004
Proceedings of Advances in Modal Logic 2004, pp. 309–333
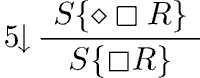
We present a cut-admissible system for the modal logic S5 in a framework that makes explicit and intensive use of deep inference. Deep inference is induced by the methods applied so far in conceptually pure systems for this logic. Thus, the formulation of a system in such a framework is an evolutional process and leads to positive proof theoretical results. The system enjoys systematicity and modularity, two important properties that seek satisfaction from modal systems. Furthermore, it enjoys a simple and direct design: the rules are few and the modal rules are in exact correspondence to the modal axioms.
Pdf 1 March 2006
Studia Logica, Vol. 85 (2) 2007, pp. 199–214
The sequent calculus does not seem to be capable of supporting cut-admissible formulations for S5. Through a survey on existing cut-admissible systems for this logic, we investigate the solutions proposed to overcome this defect. Accordingly, the systems can be divided into two categories: in those which allow semantic-oriented formulae and those which allow formulae in positions not reachable by the usual systems in the sequent calculus. The first solution is not desirable because it is conceptually impure, that is, these systems express concepts of frame semantics in the language of the logic.
Consequently, we focus on the systems of the second group for which we define notions related to deep inference—the ability to apply rules deep inside structures—as well as other desirable properties good systems should enjoy. We classify these systems accordingly and examine how these properties are affected in the presence of deep inference. Finally, we present a cut-admissible system for S5 in a formalism which makes explicit use of deep inference, the calculus of structures, and give reasons for its effectiveness in providing good modal formulations.
Pdf 20 October 2004
MSc thesis, successfully defended on 27.10.2004

Much of the success of modal logic can be attributed to the adoption of relational semantics. Consequently, modal logic is seen as logic of relational structures, where logical axioms correspond to structural properties. Alex Simpson, in his 1993 PhD thesis, introduced a labelled proof theory for modal logic that that allows cut-elimination for a class of modal logics, which is characterised by so called geometric theories. This includes important and well know logics such as M, B, S4 and S5. This thesis tries to make a bridge between Simpson's result and purely symbolic proof theory. We introduce a method to characterise frame relational properties by means of deep inference in the Calculus of Structures. The results are only partial. Only what we call 3/4-Scott-Lemmon logics are characterised and we only give plausible reason, rather than a proof that the cut-elimination argument can be transferred too.
Gzipped postscript 20 March 2005
MSc thesis, successfully defended on 23.3.2005
We divide attempts to give the structural proof theory of modal logics into two kinds, those pure formulations whose inference rules characterise modality completely by means of manipulations of boxes and diamonds, and those labelled formulations that leverage the use of labels in giving inference rules. The widespread adoption of labelled formulations is driven by their ability to model features of the model theory of modal logic in its proof theory.
We describe here an approach to the structural proof theory of modal logic that aims to bring under one roof the benefits of both the pure and the labelled formulations. We introduce two proof calculi, one labelled sequent formulation and one pure formulation in the calculus of structures that are shown to be in a systematic correlation, where the latter calculus uses deep inference with shaped modal rules to capture in a pure manner the manipulations that the former calculations mediates through the use of labels.
We situate this work within a larger investigation into the proof theory of modal logic that solves problems that existed with the earlier investigation based on prefix modal rules. We hold this development provides yet stronger evidence justifying the claim that good, pure proof theory for modal logic needs deep inference.
Pdf 25 June 2005
Proceedings of Structures and Deduction '05, pp. 126–143

We see a systematic set of cut-free axiomatisations for all the basic normal modal logics formed by some combination the axioms d, t, b, 4, 5. They employ a form of deep inference but otherwise stay very close to Gentzen’s sequent calculus, in particular they enjoy a subformula property in the literal sense. No semantic notions are used inside the proof systems, in particular there is no use of labels. All their rules are invertible and the rules cut, weakening and contraction are admissible. All systems admit a straightforward terminating proof search procedure as well as a syntactic cut elimination procedure.
Conference version pdf 30 March 2006
Proceedings of Advances in Modal Logic 2006, pp. 107–119
Full paper pdf 21 August 2007
This paper describes work in progress on using deep inference for designing a deductive system for hybrid logic. We will see a cut-free system and prove its soundness and completeness. An immediate observation about the system is that there is no need for additional rewrite rules as in Blackburn’s tableaux, nor substitution rules as in Seligman’s sequent system.
Pdf 15 May 2007
Proceedings of International Workshop on Hybrid Logic 2007 (HyLo 2007), pp. 13–22
31.8.2007 Alessio Guglielmi email