These are the notes for a 5-lecture-course given at ESSLLI 2006 in Malaga, Spain. The URL of the school is http://esslli2006.lcc.uma.es/. The course is intended to be introductory. That means no prior knowledge of proof nets is required. However, the student should be familiar with the basics of propositional logic, and should have seen formal proofs in some formal deductive system (e.g., sequent calculus, natural deduction, resolution, tableaux, calculus of structures, Frege-Hilbert-systems, ...). It is probably helpful if the student knows already what cut elimination is, but this is not strictly necessary. In these notes, I will introduce the concept of “proof nets” from the viewpoint of the problem of the identity of proofs. I will proceed in a rather informal way. The focus will be more on presenting ideas than on presenting technical details. The goal of the course is to give the student an overview of the theory of proof nets and make the vast amount of literature on the topic easier accessible to the beginner. For introducing the basic concepts of the theory, I will in the first part of the course stick to the unit-free multiplicative fragment of linear logic because of its rather simple notion of proof nets. In the second part of the course we will see proof nets for more sophisticated logics.

Pdf 20 October 2006
Technical Report 6013, INRIA

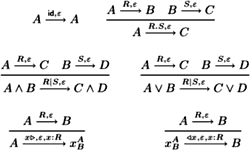
I will discuss the two problems of how to define identity between logics and how to define identity between proofs. For the identity of logics, I propose to simply use the notion of preorder equivalence. This might be considered to be folklore, but is exactly what is needed from the viewpoint of the problem of the identity of proofs: If the proofs are considered to be part of the logic, then preorder equivalence becomes equivalence of categories, whose arrows are the proofs. For identifying these, the concept of proof nets is discussed.

Pdf 8 April 2005
Logica Universalis—Towards a General Theory of Logic, pp. 135–145, Birkhäuser, 2005

We present a theory of proof denotations in classical propositional logic. The abstract definition is in terms of a semiring of weights, and two concrete instances are explored. With the Boolean semiring we get a theory of classical proof nets, with a geometric correctness criterion, a sequentialization theorem, and a strongly normalizing cut-elimination procedure. With the semiring of natural numbers, we obtain a sound semantics for classical logic, in which fewer proofs are identified. Though a "real" sequentialization theorem is missing, these proof nets have a grip on complexity issues. In both cases the cut elimination procedure is closely related to its equivalent in the calculus of structures, and we get "Boolean" categories which are not posets.

Pdf 31 January 2005
TLCA 2005, LNCS 3461, pp. 246–261

By Boolean category we mean something which is to a Boolean algebra what a category is to a poset. We propose an axiomatic system for Boolean categories, which is different in several respects from the ones proposed recently. In particular everything is done from the start in a *-autonomous category and not in a weakly distributive one, which simplifies issues like the Mix rule. An important axiom, which is introduced later, is a "graphical" condition, which is closely related to denotational semantics and the Geometry of Interaction. Then we show that a previously constructed category of proof nets is the free "graphical" Boolean category in our sense. This validates our categorical axiomatization with respect to a real-life example. Another important aspect of this work is that we do not assume a-priori the existence of units in the *-autonomous categories we use. This has some retroactive interest for the semantics of linear logic, and is motivated by the properties of our example with respect to units.

Conference version pdf 8 April 2005
Proceedings of LICS 2005, pp. 209–218

Full paper pdf 18 February 2005

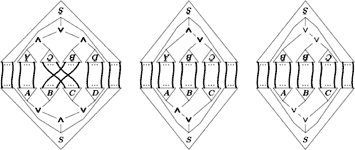
We will see how derivations in (a variation of) SKS can be translated into proof nets. Since an SKS derivation contains more information about a proof than the corresponding proof net, we observe a loss of information which can be understood as "eliminating bureaucracy". Technically this is achieved by cut reduction on proof nets. As an intermediate step between the two extremes, SKS derivations and proof nets, we will see nets representing derivations in "Formalism A".

Postscript 13 April 2005
Proceedings of Structures and Deduction '05, pp. 2–18

We call irrelevant information in derivations bureaucracy. An example of such irrelevant information is the order between two consecutive inference rules that trivially permute. Building on ideas by Guglielmi, we identify two forms of bureaucracy that occur in the calculus of structures (and, in fact, in every non-trivial term rewriting derivation). We develop term calculi that provide derivations that do not contain this bureaucracy. We also give a normalisation procedure that removes bureaucracy from derivations and find that in a certain sense the normalisation process is a process of cut elimination.

Pdf 10 June 2005
Proceedings of Structures and Deduction '05, pp. 69–80

Deep inference is a proof-theoretic notion in which proof rules apply arbitrarily deeply inside a formula. We show that the essence of deep inference is the bifunctoriality of the connectives. We demonstrate that, when given an inequational theory that models cut-reduction, a deep inference calculus for classical logic (SKSg) is a categorical model of the classical sequent calculus LK in the sense of Führmann and Pym. We observe that this gives a notion of cut-reduction for derivations in SKSg, for which the usual notion of cut in SKSg is a special case. Viewing SKSg as a model of the sequent calculus uncovers new insights into the Craig interpolation lemma and intuitionistic provability.

Pdf 31 March 2005
Proceedings of Structures and Deduction '05, pp. 19–33

This thesis introduces the notion of a classical doctrine: a semantics for proofs in first-order classical logic derived from the classical categories of Führmann and Pym, using Lawvere’s notion of hyperdoctrine. We introduce a hierarchy of classes of model, increasing in the strength of cut-reduction theory they model; the weakest captures cut reduction, and the strongest gives De Morgan duality between quantifiers as an isomorphism. Whereas classical categories admit the elimination of logical cuts as equalities, (and cuts against structural rules as inequalities), classical doctrines admit certain logical cuts as inequalities only. This is a result of the additive character of the quantifier introduction rules, as is illustrated by a concrete model based on families of sets and relations, using an abstract Geometry of Interaction construction.

We establish that each class of models is sound and complete with respect to the relevant cut-reduction theory on proof nets based on those of Robinson for propositional classical logic. We show also that classical categories and classical doctrines are not only a class of models for the sequent calculus, but also for deep inference calculi due to Brünnler for classical logic. Of particular interest are the local systems for classical logic, which we show are modelled by categorical models with an additional axiom forcing monoidality of certain functors; these categorical models correspond to multiplicative presentations of the sequent calculus with additional additive features.

Pdf 30 March 2006
PhD thesis, successfully defended on 17.3.2006

In this paper we present a theory of proof nets for full multiplicative linear logic, including the two units. It naturally extends the well-known theory of unit-free multiplicative proof nets. A linking is no longer a set of axiom links but a tree in which the axiom links are subtrees. These trees will be identified according to an equivalence relation based on a simple form of graph rewriting. We show the standard results of sequentialization and strong normalization of cut elimination. Furthermore, the identifications enforced on proofs are such that the proof nets, as they are presented here, form the arrows of the free (symmetric) *-autonomous category.

Pdf 30 June 2004
CSL 2004, LNCS 3210, pp. 145–159

In the first part of this paper we present a theory of proof nets for full multiplicative linear logic, including the two units. It naturally extends the well-known theory of unit-free multiplicative proof nets. A linking is no longer a set of axiom links but a tree in which the axiom links are subtrees. These trees will be identified according to an equivalence relation based on a simple form of graph rewriting. We show the standard results of sequentialization and strong normalization of cut elimination. In the second part of the paper we show that the identifications enforced on proofs are such that the class of two-conclusion proof nets defines the free *-autonomous category.

Pdf 5 October 2006 Journal version of On Proof Nets for Multiplicative Linear Logic with Units
Logical Methods in Computer Science, Vol. 2 (4:3) 2006, pp. 1–44

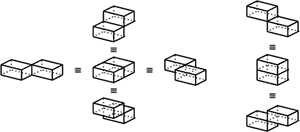
In this document, we study a 3-polygraphic translation for the proofs of SKS, a formal system for classical propositional logic. We prove that the free 3-category generated by this 3-polygraph describes the proofs of classical propositional logic modulo structural bureaucracy. We give a 3-dimensional generalization of Penrose diagrams and use it to provide several pictures of a proof. We sketch how local transformations of proofs yield a non contrived example of 4-dimensional rewriting.

Conference version 14 April 2005
Proceedings of Structures and Deduction '05, pp. 35–52

Full paper pdf 18 November 2005
Annals of Pure and Applied Logic, Vol. 141 (1-2) 2006, pp. 266–295

This paper links deep inference proof theory, as studied by Guglielmi et. al., to categorical proof theory in the sense of Lambek et. al. It observes how deep inference proof theory is categorical proof theory, minus the coherence diagrams/laws. Coherence yields a ready-made and well studied notion of equality on deep inference proofs. The paper notes a precise correspondence between the symmetric deep inference system for multiplicative linear logic (the linear fragment of SKSg and the presentation of *-autonomous categories as symmetric linearly distributive categories with negation. Contraction and weakening in SKSg corresponds precisely to the presence of (co)monoids.

Pdf 6 October 2004

We examine ‘weak-distributivity’ as a rewriting rule ^WD→ defined on multiplicative proof-structures (so, in particular, on multiplicative proof-nets: MLL). This rewriting does not preserve the type of proofs-nets, but does nevertheless preserve their correctness. The specific contribution of this paper, is to give a direct proof of completeness for ^WD→: starting from a set of simple generators (proof-nets which are a n-ary ⊗ of ℘-ized axioms), any mono-conclusion MLL proof-net can be reached by ^WD→ rewriting (up to ⊗ and ℘ associativity and commutativity).

Pdf 8 July 2005
Proceedings of Structures and Deduction '05, pp. 81–94
Submitted
Invited talk at WoLLIC 2003, under the title 'Calculus of Structures and Proof Nets', Electronic Notes in Theoretical Computer Science 84

In its most general meaning, a Boolean category is to categories what a Boolean algebra is to posets. In a more specific meaning a Boolean category should provide the abstract algebraic structure underlying the proofs in Boolean Logic, in the same sense as a Cartesian closed category captures the proofs in intuitionistic logic and a *-autonomous category captures the proofs in linear logic. However, recent work has shown that there is no canonical axiomatisation of a Boolean category. In this work, we will see a series (with increasing strength) of possible such axiomatisations, all based on the notion of *-autonomous category. We will particularly focus on the medial map, which has its origin in an inference rule in KS, a cut-free deductive system for Boolean logic in the calculus of structures. Finally, we will present a category proof nets as a particularly well-behaved example of a Boolean category.

Conference version pdf 21 June 2006
Accepted at Cl&C '06 (satellite workshop of ICALP '06), under the title 'What Could a Boolean Category Be?'

Full paper pdf 10 April 2006
To appear on Theory and Applications of Categories

The Medial rule was first devised as a deduction rule in the Calculus of Structures. In this paper we explore it from the point of view of category theory, as additional structure on a *-autonomous category. This gives us some insights on the denotational semantics of classical propositional logic, and allows us to construct new models for it, based on suitable generalizations of the theory of coherence spaces.

Pdf 27 June 2006
To appear on Theory and Applications of Categories