Counterexamples
Alessio Guglielmi's Research and Teaching / Deep Inference / Counterexamples

Finding counterexamples is one of the funniest sides of our activity. They are typically of a very combinatorial nature, due to the new combinatorial possibilities offered by deep inference.
In the calculus of structures, it is possible to replace the contraction rule by its atomic version. The same is not possible in the sequent calculus, as shown by the following counterexample due to Kai Brünnler. Looking for atomic contraction in an additive presentation of classical logic makes no sense, since non-atomic contraction is intrinsic in additive context management; for a multiplicative system, just consider
|- a ∧ b, (-a ∨ -b) ∧ (-a ∨ -b) ;
there is no way of proving this sequent by just using atomic contraction. A more thorough exposition is in the paper Two Restrictions on Contraction.
In the calculus of structures, it is possible to move all contraction instances to the bottom of any derivation. The same is not possible in the sequent calculus, as shown by the following counterexample due to Kai Brünnler. It only makes sense to check the property for a multiplicative presentation of classical logic. In such a case, it suffices to check the following sequent:
|- a ∧ a, -a ∧ -a .
A more thorough exposition is in the paper Two Restrictions on Contraction.
Kai Brünnler found that system
(KS \ {ac↓}) U {ac↑}
is incomplete. Consider in fact the valid formula
[ ( [a,b] , [-c,(a,b)] ) , (-a,-d) , ( [(c,d),-b] , [c,d] ) ] .
It is not provable in the system, as shown by the following argument.
Note that there are three conjunctions: left, middle and right. To simplify the case analysis, note that the formula is symmetric with respect to the comma in the middle conjunction.
Rules ai↓ and ac↑ don't apply.
Rule aw↓ applies in twelve cases, because of symmetry it suffices to check six ones, in every case there is a countermodel for the premise.
Medial applies in two cases, for symmetry we just check the one where it applies in the left conjunction. We have two subcases corresponding to two ways in which the medial is applied, in both cases there is a countermodel for the premise.
Switch applies 1) inside the left conjunction (inside the right conjunction is symmetric), 2) bringing together left and middle conjunction (bringing together right and middle is symmetric), 3) bringing together left and right conjunction, and 4) bringing two conjunctions into the third. All these cases have subcases corresponding to the ways in which the switch can be applied. It's tedious but easy to check that for all these cases, there is a countermodel for the premise.
Definition A binary tautology is a classical propositional tautology which, for every atom a, contains at most one positive and at most one negative occurrence of a. Let's call M the language of formulas which are substitutional instances of binary tautologies.
For example, [-a,a,a] is in M because it is a substitutional instance of the binary tautology [-b,c,b]. On the other hand, [-a,(a,a)] is not in M.
Let us now consider the system obtained from KS by removing atomic contraction, which we call BKS.
Definition System BKS is
t (R,[T,U]) [(R,U),(T,V)] f
ai_ ------ , s --------- , m ------------- , aw_ --- ;
[a,-a] [(R,T),U] ([R,T],[U,V]) a
the usual conventions apply: rules are deep, t and f are units, conjunction (...) and disjunction [...] are associative and commutative, the equations (f,f) = f and [t,t] = t may be used, and Augustus takes care of negation.
Problem Prove or disprove that BKS proves M.
Lutz Straßburger proved that BKS does not prove M. In fact, consider the following structure (in SKS notation):
[ ( [ a, b, c] , [ d, e, f] , [ g, h, j] ) , ( [ k, l,-a] , [ m, n,-d] , [ o, p,-g] ) , ( [ q,-b,-k] , [ r,-e,-m] , [ s,-h,-o] ) , ( [-c,-l,-q] , [-f,-n,-r] , [-j,-p,-s] ) ]
It is a tautology; it is easily seen to be binary; hence it is in M. It is not provable in BKS. Any rule application leads immediately to a formula which is not a tautology. Therefore BKS does not prove M.
We can obtain modal logic K4 by extending KS with the rules
S{![R,T]} S{??R}
k_ --------- , 4_ ------
S[!R,?T] S{?R}
and the equalities
t = !t and f = ?f ,
where ! and ? respectively represent box and diamond. One wonders whether K4 would be captured by KS plus the equations above and the rules
S{![R,T]} S{!R}
k_ --------- , 4^ ------ .
S[!R,?T] S{!!R}
The reason for trying this is the fact that rule 4^ is (logically equivalent to but) better than 4_ in proof search. However, the resulting system would not be complete, because the structure
S = [ ?-a , ?-b , !(!a,!b) ] ,
found by Robert Hein, is a theorem of K4 but is not provable in the system. In fact, any proof of S must include applications of the 4^ rule, since S is not a theorem of K and system KS + {k_} is sound and complete for logic K. However, when going bottom-up in looking for a proof, we observe that we can only apply 4^ to !!t and its equivalents (obtained by using the equations of KS). Moreover, none of the other rules can create a new ! or pull !s out of a conjunction. We can prove S with 4_ as follows:
t i_ -------------------------- ![ ?-a , ?-b , (!a,!b) ] k_ -------------------------- [ ??-a ,![?-b , (!a,!b)]] k_ -------------------------- [ ??-a , ??-b , !(!a,!b) ] 4_ -------------------------- [ ??-a , ?-b , !(!a,!b) ] 4_ -------------------------- . [ ?-a , ?-b , !(!a,!b) ]
This is one of the most remarkable structures I have ever seen. It is due to Alwen Tiu and it shows that the sequent calculus, or any other formalism based on shallow inference, cannot represent the logic BV. The counterexample consists of a fantastic logical fractal. You can find its construction, and plenty of pictures, in the paper A System of Interaction and Structure II: The Need for Deep Inference. If you know the idea already, the following picture is all you need:
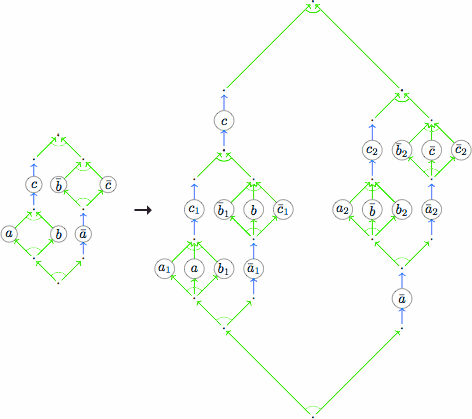
The following derivation shows that comerge does not permute over merge:
(<[a,b];c>,d)
m_ -------------
([a,b,c],d)
m^ ------------- .
[a,<[b,c];d>]
However, in view of a decomposition theorem, the situation could be fixed by the following:
(<[a,b];c>,d)
m^ -------------
<[a,b];c;d>
m_ -------------
<[a,b,c];d>
m_ ------------- .
[a,<[b,c];d>]
The following counterexample by Alwen Tiu shows that actually the fix does not work in general. Consider:
( < [<a;c>,f] ; [d,g]> , <b;e> )
m_ --------------------------------
( [ <a;c;d> , <f;g> ] , <b;e> )
m^ --------------------------------- .
[ < (a,b) ; (<c;d>,e) > , <f;g> ]
Lutz Straßburger found that it is not possible to push (atomic) interaction to the top of a proof in system BV. The following structure is provable in BV:
[ < ([d,-d],<a;b>) ; c > , < -a ; (<-b;-c>,[e,-e]) > ] .
However, it cannot be proved, building a proof bottom-up, by first applying only switch and seq, and then only interaction; interaction can only be pushed to the top of the proof by applying a coseq first.
24.12.2004 Alessio Guglielmi email