Frequently Asked Questions
and
Useful Remarks for Referees

Alessio Guglielmi's Research and Teaching / Deep Inference / Frequently Asked Questions and Useful Remarks for Referees

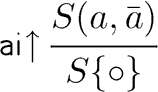
Please do not hesitate to ask questions, either by an email to me, or, even better, by using our mailing list.
It's deducing inside a formula, or structure, at any depth. Sequent calculus rules only see the root of formulae, what we call 'shallow inference'; rules in the calculus of structures, instead, can rewrite at any position in the formula tree.
It's a formula modulo an equivalence relation: it can be thought of as a sequent, which usually is an expression modulo associativity, commutativity, etc. We do not call it 'sequent' because we abolish the distinction between formulae and sequents, so the structure is sort of an intermediate kind of object.
This term is used in many places, but there is a tradition in philosophical proof theory which uses 'structure' the same way we do. In addition, in a certain sense, all our inference rules are 'structural' in the general proof theoretical meaning. In fact, we have no connectives: our expressions are sets plus structure, they are not very different from semantic structures in the usual sense.
Not as much as we'd like to: we have our fair share of lengthy case analyses, but luckily we can prove very elegant theorems. On the other hand, some of our proofs are very compact, much better than their counterparts in the sequent calculus, for example cut elimination and consistency for classical logic.
No! It happened that the first system studied in the calculus of structures (system BV) required (the analogous of) the mix rule, but that's it. All other systems do without, unless one explicitly wants (the analogue of) mix.
This is not a problem. For example, if you have a complete system for a logic in the sequent calculus, you can simulate it inside the calculus of structures. Take, say, sequent system LK for classical logic: it is faithfully simulated by system KS in the calculus of structures, without additional cost in complexity. This means that you can use LK as a complete strategy inside the proof search space induced by KS, and this gives you the same nondeterminism you have in the sequent calculus. Actually, the situation is much better than this: many deductive systems are simulated at no cost inside the calculus of structures, like for example resolution. So, you might think of mixing several different strategies, and this can further improve on the amount of nondeterminism. Finally, a new class of theorems (called 'splitting' theorems) allow for a systematic design of new strategies inside the search space; this is an active area of research.
No, we are not cheating. The equations are exclusively used in correspondence of invertible, linear inference rules. These inference rules do not alter the geometry of proofs, in the sense of relation webs, proof nets and atomic flows, for example. So, it is convenient to work on formulae modulo these equations, because we get much closer to the semantics of proofs. This comes at the expense of an immediate understanding of the calculus of structures in terms of proof search. However, fully syntactic systems can be obtained by simply turning equations into inference rules, and this only blows polynomially the size of proofs, without destroying any good property, like locality and normalisability, for example.
No, proof nets are top-down asymmetric: they consist of trees with some links on top (in the simplest case of multiplicative linear logic). There is yet no notion which flips nets upside-down and at the same time produces a dual net. On the other hand, we are working towards bringing the calculus of structures top-down symmetry to proof nets, so making it possible to deal with nets characterising derivations, which are more general objects than proofs.
No, the calculus of structures uses deep inference, abolishes the distinction between formula and sequent and exploits a symmetry between premiss and conclusion in inference rules: these are not features of the sequent calculus and they require new techniques.
There are other formalisms which use deep inference, but none (as far as we know) allows for the same kind of proof-theoretical analysis of the sequent calculus, for example cut elimination. The only exception is Schütte's presentation of logic, which uses deep inference, but doesn't drop the distinction between formula and sequent and does not exploit a premiss-conclusion symmetry (for example, its cut rule has two premisses). The proof theory of Schütte doesn't differ significantly from the usual (Gentzen) one, and does not achieve more.
One can argue that the display calculus uses a form of deep inference, but again the two other features of the calculus of structures are not exploited.
For systems with involutive negation, yes. In this case one can trivially translate a system in the sequent calculus into an isomorphic one in the calculus of structures which has an isomorphic proof theory: it would just be a change of notation. Of course, the point is that one can do more than just this.
For systems without involutive negation, like intuitionistic logic, it is possible to use the calculus of structures in its present form by using polarities, or asymmetric logical relations like implication.
It is certainly possible to generalise the calculus of structures in such a way that it can deal trivially with any system in the sequent calculus, irrespective of negation. We don't know how many of the new properties could be retained in such a case, but we conjecture that most of them would be preserved, so this appears to be an interesting research direction for the future.
Wrong, and the answer doesn't even depend on the notion of bureaucracy you use. Since you can design systems in the calculus of structures which completely and faithfully mimic systems in the sequent calculus, the bureaucracy is at worse the same as in the sequent calculus, no matter which notions you use. However, since in the calculus of structures you have access to deep inference, you can design inference rules which are much more efficient than what is possible in shallow inference, and this reduces bureaucracy. This is most prominently testified by the fact that in the calculus of structures there are classes of proofs which are exponentially shorter than proofs of the same sentences in the sequent calculus.
Of course atomic cut is sound and admissible for the sequent calculus, as a direct consequence of the cut elimination theorem. Still we make a big deal of our atomic cut, for two reasons:
First, for reducing generic cuts to atomic cuts in the sequent calculus one has to go through the cut elimination procedure, which is in general complex. On the contrary, in the calculus of structures the reduction is trivial and local (i.e., rewriting only occurs in a bounded portion of the proof). We exploit the nice consequences of this easy reduction, and in particular we prove cut elimination thanks to it, and not the other way round.
Second, in the sequent calculus the reduction of cut to atomic form only works for proofs (i.e., derivations without premisses). In the calculus of structures, the reduction works in any derivation. As a consequence, we can prove decomposition theorems, i.e., statements about the constructive existence of several nice normal forms based on the partitioning of formal systems into disjoint fragments.
Our deductive systems are very different than those in the sequent calculus, so cut elimination is not a trivial issue. We can prove cut elimination by resorting to the sequent calculus through a translation, but we are also interested in doing so directly inside the calculus of structures. The reasons for doing so are: 1) it's very challenging, due to deep inference; 2) it opens new perspectives for computational interpretations. For example, we are able to type diagrams associated to beta reductions with sharing much better than other formalisms can do.
One of the favourite activities of mathematicians is trying to render more and more trivial the proofs of important old statements. This activity is more than just a sport, it leads to better understanding a subject and often to applications. It's also known that finding easy proofs is very difficult.
We are sorry if you feel offended by us remarking so obvious common sense facts, but we had a referee report from somebody complaining about an almost trivial cut elimination proof not being enough for a paper.
No. Our cut-free systems enjoy the finite choice property, which means that given a conclusion, every inference rule yields a finite set of possible premisses. This is the essence of the subformula property. Technically speaking, the subformula property is meaningless for our systems (and so they don't enjoy it). The reason is our abolishing the distinction between formula and sequent, i.e., the distinction between object and meta (or judgmental, structural) level in derivations.
Essentially, yes (one has to be a bit careful and give different type to variables for atoms and variables for generic structures). Deep inference naturally corresponds to rewriting in a term rewriting system, shallow inference requires the (less natural) constraining of rewriting to the root of terms.
Because we are actually doing proof theory, and it is easier to address typical proof theoretical problems by using as close as possible a terminology to the one already in use. Moreover, in term rewriting one has to choose in which direction rewriting occurs, while derivations can be considered as growing both from top to bottom and from bottom to top.
Rewriting logic also employs term rewriting modulo equational theories, but its purpose is very different from ours. Rewriting logic is an extremely general formalism, which is more about describing uniformly and implementing many different systems than performing concrete proof theoretical investigations. On the other hand, there exist now several implementations of our deductive systems in Maude, which is an offspring of rewriting logic.
So far, no. We have no philosophical analysis backing our investigation. But we are strongly guided by aesthetic principles: our rules are very simple and they all come from common simple schemes, irrespective of the logical systems they belong to. This cannot be a coincidence and we believe that in due time an appropriate philosophical justification will be found. For now, we content ourselves of studying the many new proof theoretical properties that are made possible in our formalism.
8.9.2007 Alessio Guglielmi email